Documentation utilisateur de Manuscreen
Vous trouverez en dessous la documentation utilisateur de Manuscreen, vous pouvez la lire ici ou la télécharger pour l’emmener partout avec vous ! Des tutoriels sont disponibles ici !
Vous trouverez en dessous la documentation utilisateur de Manuscreen, vous pouvez la lire ici ou la télécharger pour l’emmener partout avec vous ! Des tutoriels sont disponibles ici !
Notre jeu, intitulé “Une intéressante épopée de Monsieur Paf“, est né suite à des expérimentations autour du concept de l’isométrie 2D. Comme la 3D n’était pas compatible avec nos envies et nos choix artistiques, l’idée originale était d’essayer de gérer un axe vertical en plus du plan horizontal dans le but de pouvoir créer des ponts ou autres éléments avec lesquels les personnages pourraient à la fois marcher dessus ou bien passer en dessous. Au fil de nos tests, le résultat devenant de plus en plus convainquant, nous avons donc développé un gameplay autour de ce moteur en même temps que nous le développions.
J’ai été très surpris en lisant l’article de Martin Pane sur la création de leur jeu en isométrie 2D. Son approche de la problématique est très intéressante et en même temps très différente de la mienne car il ne semble pas du tout utiliser le concept de TileMap, et de fait, les performances du jeu doivent être bien meilleures. Mon approche, quant à elle, est beaucoup plus conventionnelle et inspirée de tutoriels et autres exemples trouvés sur le web. C’est pourquoi, dans un esprit de partage et pour faire écho à ses réflexions, j’ai décidé de donner un aperçu de mon travail en espérant que cela inspirera d’autres projets. A vous ensuite de choisir la méthode la plus adaptée, voire même de faire un mix des deux.
Avant tout, si vous souhaitez créer un platformer isométrique, je ne saurais trop vous conseiller de vous orienter vers la 3D plutôt que vers une approche 2D. Vous réduirez ainsi considérablement le temps de développement en utilisant une caméra orthographique, en bénéficiant de la physique et des autres outils très puissants proposés de base sur Unity, et le résultat en sera d’autant plus optimisé. Cependant, si vous ne pouvez pas ou ne voulez pas, mais vraiment pas, travailler en 3D, alors ce qui suit pourra peut-être vous être utile.
La méthode classique pour créer un univers en isométrie 2D passe par l’utilisation d’une TileMap. Ce principe vous permet de simuler une vue 3D à partir d’un système de coordonnées en 2D. Vous trouverez beaucoup de tutoriels expliquant son fonctionnement sur le web. C’est un concept presque aussi vieux que le jeu vidéo, c’est pourquoi je ne m’attarderai pas sur ce sujet et les théories qui en découlent.
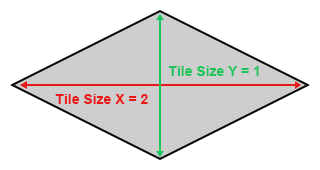
Pour notre moteur isométrique, nous avons choisi d’utiliser des tuiles (ou « tiles ») en forme de losange avec un ratio de 2/1 :
Ensuite nous avons défini l’origine et les axes isométriques de manière à rester cohérent avec ce qui se fait couramment dans un environnement 3D :
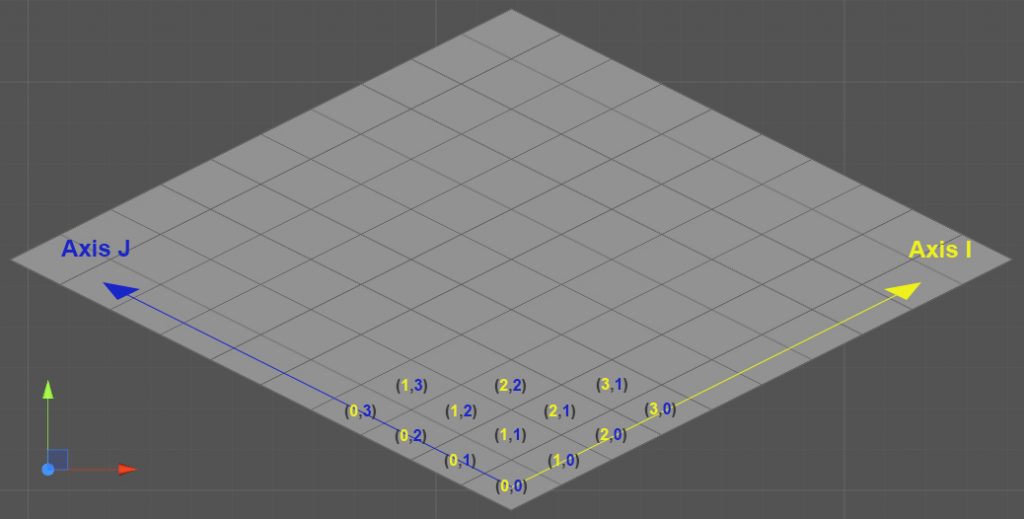
J’ai ensuite ajouté un axe vertical nommé « K », définissant son unité comme la hauteur d’un cube isométrique. 1K est donc égal à la hauteur d’une tuile.Contrairement aux axes I et J qui peuvent uniquement être définis par des nombres entiers, l’axe K est un réel (ou flottant), ce qui est nécessaire pour implémenter la gravité par la suite.
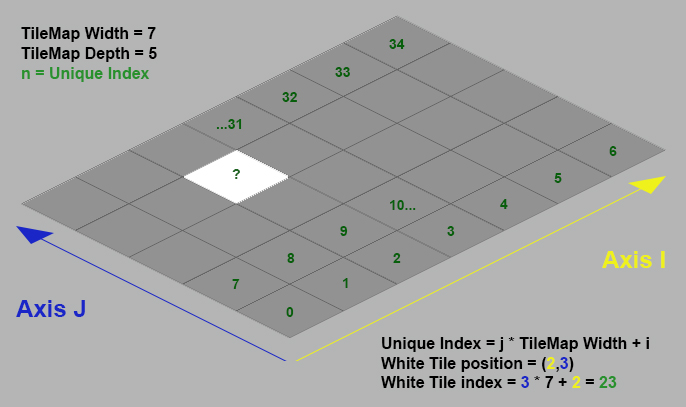
Au niveau code, on pourrait être tenté, à juste titre, de créer un tableau à deux dimensions pour référencer les tuiles. Cependant il y a une bien meilleure solution qui consiste à convertir les coordonnées isométriques (i, j) en un index entier et qui permet ainsi d’utiliser un simple tableau. La conversion est basée sur la taille de la TileMap :
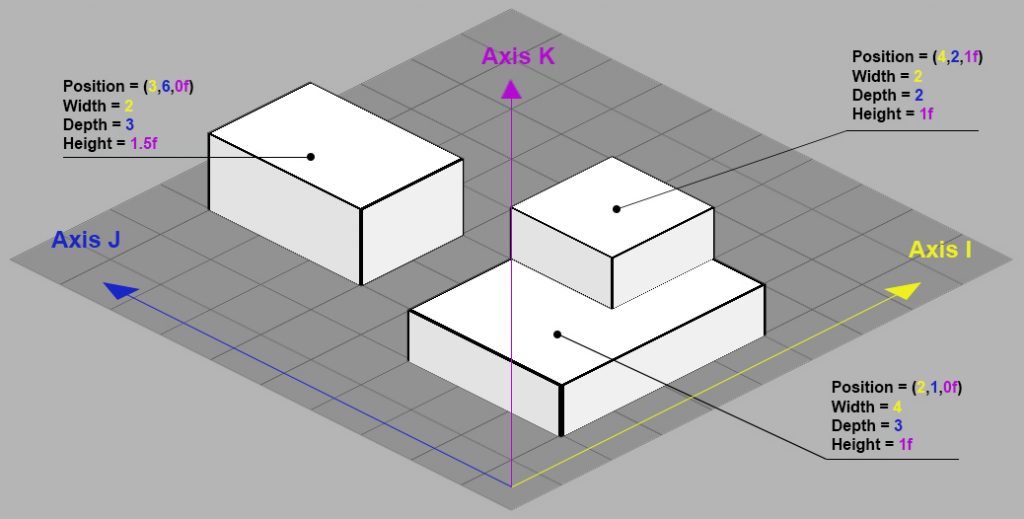
Pour définir et référencer les objets dans l’environnement isométrique, j’ai créé un composant représentatif de chaque entité indiquant sa position sur les axes [I,J,K] ainsi que sa taille. Je l’ai nommé « Mapper ». On peut alors positionner un mapper sur la scène en fonction de ses coordonnées isométriques :
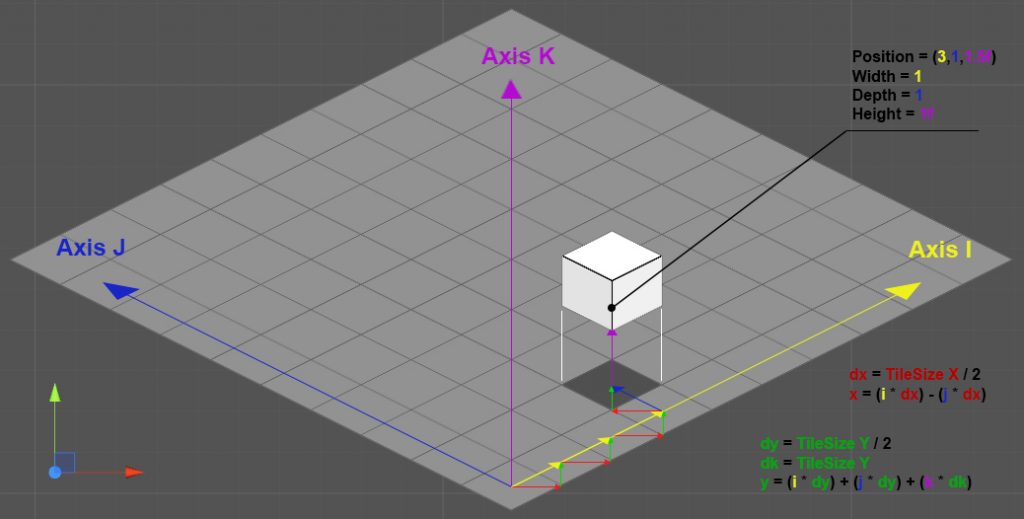
Chaque mapper est donc référencé dans l’environnement isométrique sur une ou plusieurs tuiles en fonction de sa taille. Cependant, au lieu de créer une entité (classe) pour chaque tuile, je les ai regroupée dans l’entité « TileMap » afin d’augmenter les performances. Elle ne contient donc pas un tableau d’entités « Tile » mais simplement un tableau de listes d’objets « Mapper ». La notion de tuile devient donc une simple structure CSharp (et non une classe ! Voir ici pour plus d’explications) contenant des méthodes « raccourcis » vers l’entité « TileMap ». Le code devient donc beaucoup plus rapide à l’exécution et utilise beaucoup moins de mémoire.
Une fois la « TileMap » opérationnelle, on peut alors commencer à construire notre univers. Le sprite, qui est la représentation visuelle de l’objet logique, est associé au mapper à l’aide du composant « SpriteRenderer ». J’ai également fait en sorte que d’éventuels GameObject enfants comportant un « SpriteRenderer » soient pris en compte afin que l’on puisse utiliser plusieurs sprites pour un seul mapper, et même des systèmes de particules.
Comme pour tout projet de jeu vidéo, il nous fallait un éditeur de niveau, car attendre que les images soient prêtes pour construire les niveaux n’est pas une option viable. J’ai donc créé une entité primitive qui nous permet de construire et de tester le level design sans avoir besoin d’attendre que les graphismes soient achevés.
Dans Unity, un sprite n’est ni plus ni moins qu’un plan 3D auquel on applique un « material » avec une texture. Comme tout objet 3D, il est donc défini par un mesh, soit des vertex, des triangles, et un mapping « UV ». On peut facilement le vérifier en important et en le mettant sur la scène. Changez ensuite le « Draw Mode » sur « Wireframe » pour visualiser les vertex du mesh définissant le sprite.
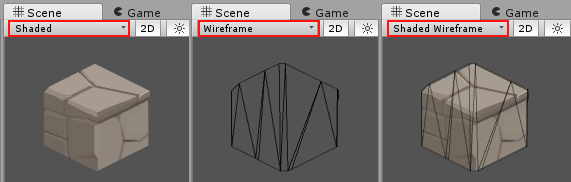
Note : il semble beaucoup plus efficace en terme de performance d’ajouter des vertex pour détourer une image plutôt que de demander au GPU de traiter un nombre important de pixels transparents. Quand vous importez une image, Unity détecte les pixels transparents et calcule automatiquement les vertex réalisant le détourage. Depuis la version 5.6, l’éditeur de sprite contient une option « Edit Outline » qui vous permet de modifier ces vertex. Cela peut être très utile si vous avez besoin de réduire le nombre de vertex et de triangles pour optimiser le temps de rendu.
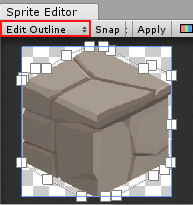
Une primitive est donc la représentation visuelle d’un cube dont on peut changer la taille et la couleur. Un cube en vue isométrique contient trois faces visibles, « Top » (haut), « Left » (gauche) et « Right » (droite). On pourrait ne créer qu’un seul mesh pour ces trois faces, mais j’ai préféré en créer un pour chaque face pour pouvoir ajouter un contour, nuancer les faces et ainsi rendre la scène plus lisible.
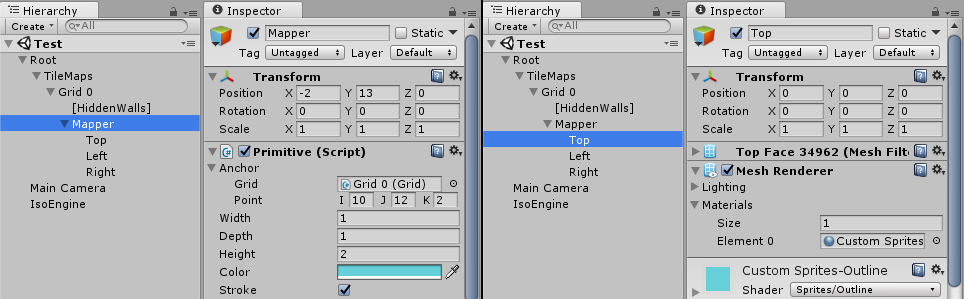
Vous trouverez plus d’information sur la création de mesh à partir du code en lisant ce post.

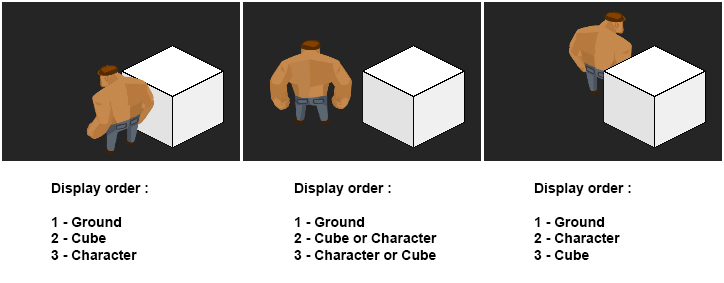
Comme l’explique Martin Pane, la priorité d’affichage lorsqu’on rend un sprite est la suivante, du plus prioritaire au moins prioritaire :
Si deux sprites ont le même « Sorting Layer » et le même « Order In Layer », celui le plus proche de la caméra sera affiché devant l’autre.
L’univers isométrique est fait de sprites 2D. Cela implique d’écrire un algorithme qui détermine l’ordre d’affichage de tous les sprites. Si tous les objets étaient statiques, cela ne serait pas très problématique, mais comme les personnages se déplacent dans cet univers, les choses deviennent bien plus compliquées.
L’ordre d’affichage est défini par la position et la taille des objets dans la « TileMap ». Il est alors possible d’établir un ordre exhaustif d’affichage des objets à partir du système de coordonnées isométrique. Cet ordre est ensuite renseigné aux composants « SpriteRenderer » par la propriété « Order In Layer » (depuis le code, cette propriété s’appelle « sortingOrder » ), allant de 0, le plus éloigné, à N, le plus proche. La position « z » du « GameObject » peut également être utilisée pour organiser les objets enfants et aussi animer un objet contenant plusieurs « Renderer ».
Note : Les propriétés d’ordre d’affichage (« sortingLayerId », « sortingLayerName », « sortingOrder », etc) ne sont pas spécifiques au composant « SpriteRenderer » mais sont héritées du composant « Renderer ». On peut donc y accéder et les modifier via le code même pour un composant « MeshRenderer » ou un système de particules. (voir ici)
Travailler en isométrie 2D peut facilement vous faire oublier que vous n’êtes pas dans un environnement 3D et donc que certaines choses ne sont pas possibles. Par exemple :

Si vous tentez de réaliser cette figure en 2D, vous allez rencontrer un problème : en considérant 1 sprite par cube, le cube bleu doit être affiché devant le vert, le cube vert devant le rouge, mais le rouge doit être devant le bleu… On se retrouve avec ce que nous avons appelé un « triangle infini », rappelant le triangle de Penrose. « Infini » car nous obtenons le résultat suivant à l’exécution du jeu :

Lorsqu’on construit les niveaux, il est assez facile de les éviter. Mais lorsque les personnages se déplacent, ils peuvent apparaître à des endroits inattendus. Au bout d’un moment, on arrive à anticiper la plupart des cas de figure, mais il y en a toujours qui nous échappent.
Afin de déterminer l’ordre d’affichage, j’ai écris plusieurs algorithme en essayant de minimiser les comparaisons entre les objets. Mais finalement, celui qui semblait être le moins performant s’est avéré être le seul réellement efficace. Il consiste en l’utilisation d’une méthode récursive qui détermine l’ordre d’affichage d’un objet après avoir déterminé celui des objets situés visuellement derrière :
//Déclaration du compteur à incrémenter
private int _currentSortingOrder = 0 ;
//Exécution à chaque frame
private void Update(){
//Récupération de la liste des mappers référencés sur la TileMap
List mappers = Tilemap.GetAllMappers() ;
//Initisation des mappers pour le rendu
for(int m=0 ; m {
//Méthode définissant la propriété « Rendered » à « false », entre autres choses
mappers[m].InitializeRendering() ;
}
//Initialisation du compteur
this._currentSortingOrder = 0 ;
//Rendu de tous les mappers
for(int m=0 ; m {
this.RenderMapper(mappers[m]) ;
}
}
private void RenderMapper(Mapper toRender)
{
//Ignore si le mapper est déjà rendu
if(toRender.rendered) return ;
//Liste les mappers situés visuellement derrière
List mappersBehind = this.GetMappersBehindOf(toRender) ;
for(int m=0 ; m {
RenderMapper(mappersBehind[m]) ;
}
//Renseigne l’ordre d’affichage au mapper et défini la propriété « rendered » à « true »
toRender.RenderAt(this._currentSortingOrder) ;
this._currentSortingOrder++ ;
}
private List GetMappersBehindOf(Mapper target)
{
//Initialisation de la liste
List mappersBehind = new List() ;
//Liste les mappers étant visuellement derrière
[…]
//Et retourne la liste
return mappersBehind ;
}
L’inconvénient de cette approche est qu’elle doit être exécutée à chaque frame. C’est pourquoi la micro-optimisation du code est de rigueur pour que l’algorithme ne soit pas trop long à l’exécution (par exemple, préférer l’utilisation d’instructions « for » au lieu de « foreach » pour autre chose qu’un tableau, ou encore éviter de boucler sur un « Dictionary ». Voir ici). Si vous voulez que le jeu tourne à 60 fps, chaque frame doit être calculée en moins de 16 millisecondes. En prenant en compte le temps de rendu de la carte graphique, d’autres algorithmes potentiellement gourmands comme le pathfinder et le fait que nous travaillons avec des machines plutôt performantes, nous avons défini un temps de calcul maximal de 10 millisecondes pour cet algorithme.
De plus, son temps d’exécution augmente en fonction du nombre d’objets, de leur taille et aussi de la taille de la TileMap. Nous nous sommes donc rapidement retrouvés limités par la taille de la TileMap. Pour une grille de 25 par 25 avec une cinquantaine d’objets situés en 0K et 7K en hauteur, nous arrivons à un temps de rendu compris entre 8 et 9 millisecondes. Si le jeu est une succession de petites pièces, cela fonctionne. Mais nous souhaitions avoir des zones relativement étendues dans lesquels le joueur pourrait se déplacer un peu comme dans un « open world » / « RPG ». Pour ce faire, nous avons trouvé une solution : le multi-TileMap.
Au lieu d’avoir une grille de 100 par 100 ayant un temps de rendu complètement absurde de 50 millisecondes, nous l’avons divisé en plusieurs TileMap d’environ 15 par 15. Chacune a donc un temps de rendu compris entre 1 et 3 millisecondes. L’astuce consiste ensuite à appliquer un second algorithme pour déterminer l’ordre d’affichage des TileMap et de ne rendre que les TileMap étant visible à lécran.
Le résultat final n’est pas si mal, et s’avère même être plutôt efficace (je l’ai testé sur mon ordinateur portable vieux de 10 ans). Mais il y aura toujours des limitations, tout dépend de comment on construit les niveaux, plus précisément de s’ils s’étendent beaucoup sur la hauteur ou non, mais aussi du gameplay, des interactions que l’on souhaite mettre en place, de la gestion de la physique et du déplacement des personnages.
A partir de là, le moteur peut être adapté à différent type de gameplay, que ce soit un pointé cliqué, un RPG, un platformer ou bien ce que vous voulez. Notre jeu étant un puzzle platformer, j’ai donc dû implémenter la physique sur l’axe vertical ainsi que la gestion des déplacements sur les axes horizontaux. Je ne doublerai pas la taille de cet article en vous expliquant comment cela fonctionne, mais je vais vous donner quand même quelques pistes :
